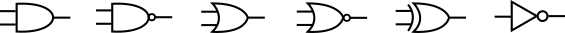Bem-vindo
Seja bem-vindo!
Este manual foi feito para aqueles que nunca estudaram sobre portas lógicas e circuitos digitais, mas tem curiosidade em aprender sobre o que está por trás de dispositivos eletrônicos.
Nos capítulos seguintes explicaremos:
- As portas lógicas básicas: como AND, OR, NOT e outras.
- Como criar circuitos combinando portas lógicas.
- Como simplificar expressões lógicas para facilitar o design de circuitos. (FUTURO)
Vamos guiar você passo a passo. No final, você estará pronto para construir seus próprios circuitos lógicos e entender como eles funcionam!
O que é álgebra booleana?
A álgebra booleana é uma área da matemática que trabalha com valores verdadeiros e falsos, geralmente representados pelos números 1 e 0, respectivamente. Ela foi criada por George Boole no século XIX e é usada para descrever operações lógicas simples que são muito importantes na eletrônica digital e na computação.
Figura 1: George Boole

Fonte: Wikipedia
Em circuitos e portas lógicas, usamos a álgebra booleana para representar e simplificar o comportamento de componentes eletrônicos que processam informações. Por exemplo, com a álgebra booleana podemos expressar como um circuito vai responder a uma combinação de entradas, como "ligado" ou "desligado", representando essas situações como 1 e 0. Isso é fundamental porque computadores e muitos dispositivos eletrônicos trabalham apenas com essas duas condições (1 e 0), e a álgebra booleana nos ajuda a entender e controlar como essas condições se combinam.
Aqui estão algumas operações básicas da álgebra booleana:
- AND (E): O resultado é 1 apenas se todas as entradas forem 1.
- OR (OU): O resultado é 1 se pelo menos uma entrada for 1.
- NOT (NÃO): Inverte o valor, ou seja, transforma 1 em 0 e 0 em 1.
Essas operações são representadas em circuitos eletrônicos pelas portas lógicas que você vai estudar, como portas AND, OR e NOT. Elas são blocos fundamentais de computadores, calculadoras e qualquer aparelho que processe dados.
Assim, entender a álgebra booleana é o primeiro passo para compreender como esses dispositivos funcionam por dentro.
Exercício: Introdução à Álgebra Booleana
- Instruções: Responda às perguntas abaixo com base nas explicações sobre as portas lógicas. Utilize seus conhecimentos sobre álgebra booleana para responder as questões.
-
O que é a álgebra booleana e quem foi seu criador?
-
Quais são os dois valores básicos usados na álgebra booleana e o que eles representam?
-
Qual operação booleana tem como resultado 1 apenas quando todas as entradas são 1?
-
Descreva a operação OR. O que acontece se uma das entradas for 1?
-
Explique a função da operação NOT na álgebra booleana. O que acontece com o valor da entrada?
-
Por que a álgebra booleana é importante na eletrônica digital e na computação?
O que são portas lógicas?
Portas lógicas são blocos fundamentais usados em circuitos eletrônicos para realizar operações lógicas básicas, como as que vimos na álgebra booleana. Elas recebem entradas, que podem ser 0 (falso) ou 1 (verdadeiro), e geram uma saída também em 0 ou 1, dependendo da operação lógica que a porta realiza. Essas portas são usadas para criar todos os tipos de sistemas digitais, como computadores, calculadoras e até celulares.
Existem diferentes tipos de portas lógicas, cada uma correspondendo a uma operação da álgebra booleana:
-
Porta AND (E): Só gera uma saída 1 (verdadeiro) quando todas as entradas são 1. Se qualquer entrada for 0, a saída será 0.
-
Porta OR (OU): Gera uma saída 1 se pelo menos uma das entradas for 1. Se todas as entradas forem 0, a saída será 0.
-
Porta NOT (NÃO): Inverte o valor da entrada. Se a entrada for 1, a saída será 0, e se a entrada for 0, a saída será 1.
Além dessas, existem portas mais avançadas como:
-
Porta NAND: O contrário da AND. Gera 0 quando todas as entradas são 1, e 1 em qualquer outro caso.
-
Porta NOR: O contrário da OR. Gera 1 quando todas as entradas são 0, e 0 se houver pelo menos uma entrada 1.
-
Porta XOR (OU exclusivo): Gera 1 se uma e apenas uma das entradas for 1, mas gera 0 se ambas as entradas forem iguais (ambas 0 ou ambas 1).
Essas portas são implementadas com transistores no nível físico e são os "tijolos" que compõem os circuitos digitais dentro dos dispositivos eletrônicos. Ao combinar várias portas lógicas, podemos criar circuitos complexos que realizam tarefas como somar números, comparar valores ou armazenar dados.
Portas
Abaixo estão uma lista de todas as portas lógcas básicas:
OR
A porta OR (OU) é uma porta lógica que realiza a operação "OU" da álgebra booleana. Ela recebe duas ou mais entradas e gera uma saída 1 (verdadeira) se pelo menos uma das entradas for 1. A saída será 0 (falsa) apenas se todas as entradas forem 0.
Ou seja: Se as entradas forem 1 e 0, a saída será 1. Se as entradas forem 0 e 0, a saída será 0.
Tabela verdade:
| A | B | Saída |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
A porta OR é usada quando queremos que a saída seja verdadeira se qualquer uma das condições for verdadeira. Em circuitos eletrônicos, ela permite que um sistema funcione mesmo que apenas uma das partes esteja ativa.
Teste a porta OR no nosso simulador (AINDA EM CONTRUÇÃO). Clique Aqui.
AND
A porta AND (E) é uma das portas lógicas mais básicas e realiza a operação "E" da álgebra booleana. Ela recebe duas ou mais entradas e só gera uma saída 1 (verdadeira) quando todas as entradas forem 1. Se qualquer uma das entradas for 0, a saída será 0 (falsa).
Ou seja: Se as entradas forem 1 e 1, a saída será 1. Se as entradas forem 1 e 0, a saída será 0.
Tabela verdade:
| A | B | Saída |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
A porta AND é usada quando queremos verificar se todas as condições são verdadeiras ao mesmo tempo. Em circuitos eletrônicos, ela é implementada para controlar situações em que todas as partes de um sistema precisam estar "ligadas" para que algo funcione.
Teste a porta AND no nosso simulador (AINDA EM CONTRUÇÃO). Clique Aqui.
XOR
A porta XOR (OU exclusivo) é uma porta lógica que realiza a operação "OU exclusivo" da álgebra booleana. Ela gera uma saída 1 (verdadeira) somente quando uma das entradas for 1, mas não ambas. Se ambas as entradas forem iguais, seja 0 e 0 ou 1 e 1, a saída será 0 (falsa).
Ou seja: Se as entradas forem 1 e 0, a saída será 1. Se as entradas forem 1 e 1, a saída será 0.
Tabela verade:
| A | B | Saída |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
A porta XOR é útil em circuitos onde queremos detectar situações em que as entradas são diferentes. Um exemplo comum é em circuitos de adição binária, onde a porta XOR é usada para determinar a soma de dois bits.
Teste a porta XOR no nosso simulador (AINDA EM CONTRUÇÃO). Clique Aqui.
NOT
A porta NOT (NÃO) é uma porta lógica simples que realiza a operação "NÃO" da álgebra booleana, também chamada de inversão. Ela tem apenas uma entrada e sua função é inverter o valor dessa entrada. Ou seja, se a entrada for 1 (verdadeira), a saída será 0 (falsa), e se a entrada for 0, a saída será 1.
Ou seja: Se a entrada for 1, a saída será 0. Se a entrada for 0, a saída será 1.
Tabela verdade:
| A | Saída |
|---|---|
| 0 | 1 |
| 1 | 0 |
A porta NOT é usada em circuitos quando precisamos inverter um sinal lógico, ou seja, transformar o "ligado" em "desligado" ou vice-versa. É uma das portas mais básicas e essenciais na construção de sistemas lógicos.
Teste a porta NOT no nosso simulador (AINDA EM CONTRUÇÃO). Clique Aqui.
NOR
A porta NOR é uma combinação das portas OR e NOT. Ela realiza a operação "OU-NÃO" da álgebra booleana, ou seja, primeiro faz a operação OR (OU) e depois inverte o resultado com uma operação NOT (NÃO). A porta NOR gera uma saída 1 (verdadeira) apenas quando todas as entradas forem 0. Se qualquer uma das entradas for 1, a saída será 0 (falsa).
Ou seja: Se as entradas forem 0 e 0, a saída será 1. Se as entradas forem 1 e 0, a saída será 0.
Tabela Verdade:
| A | B | Saída |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
A porta NOR é útil quando precisamos de um circuito que só ative a saída quando nenhuma das entradas estiver ativa (todas forem 0). Em sistemas eletrônicos, ela é usada para condições de negação geral, onde todas as entradas precisam estar "desligadas" para que o sistema funcione.
Teste a porta NOR no nosso simulador (AINDA EM CONTRUÇÃO). Clique Aqui.
NAND
A porta NAND é uma combinação das portas AND e NOT. Ela realiza a operação "E-NÃO" da álgebra booleana, ou seja, primeiro faz a operação AND (E) e depois inverte o resultado com uma operação NOT (NÃO). A porta NAND gera uma saída 0 (falsa) apenas quando todas as entradas forem 1. Se qualquer uma das entradas for 0, a saída será 1 (verdadeira).
Ou seja: Se as entradas forem 1 e 1, a saída será 0. Se as entradas forem 1 e 0, a saída será 1.
Tabela verdade:
| A | B | Saída |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
A porta NAND é muito importante porque pode ser usada para construir qualquer outra porta lógica. Isso significa que, com apenas portas NAND, podemos criar circuitos lógicos complexos. Ela é muito comum em circuitos digitais por sua versatilidade e simplicidade.
Teste a porta NAND no nosso simulador (AINDA EM CONTRUÇÃO). Clique Aqui.
Exercício: Entendendo as Portas Lógicas
- Instruções: Responda às perguntas abaixo com base nas explicações sobre as portas lógicas. Utilize seus conhecimentos sobre as portas AND, OR, NOT, XOR, NAND e NOR para resolver os problemas.
-
Sobre Porta AND (E):
- a) Se as entradas de uma porta AND forem 1 e 0, Qual será a saída?
- b) Agora, considere que as entradas são 1 e 1. Qual será a saída?
-
Sobre Porta OR (OU):
- a) Para uma porta OR com entradas 0 e 1, qual será a saída?
- b) O que acontece se as entradas forem 0 e 0?
-
Sobre Porta XOR (OU exclusivo):
- a) Em uma porta XOR, o que acontece com as entradas 1 e 1? Qual será a saída?
- b) Se as entradas forem 1 e 0, qual é o valor da saída?
-
Sobre Porta NOT (NÃO):
- a) Se a entrada de uma porta NOT for 1, qual será a saída?
- b) E se a entrada for 0?
-
Sobre Porta NOR (OU-NÃO):
- a) Uma porta NOR tem as entradas 0 e 0. Qual será a saída?
- b) O que acontece se uma das entradas for 1?
-
Sobre Porta NAND (E-NÃO):
- a) Se uma porta NAND recebe 1 e 1 como entradas, qual será a saída?
- b) Se as entradas forem 1 e 0, qual será o valor da saída?
Introdução a circuitos lógicos
Os circuitos lógicos são conjuntos de componentes eletrônicos interconectados que realizam operações lógicas usando portas lógicas. Esses circuitos processam informações binárias, representadas por 0s e 1s, e são a base de sistemas digitais, como computadores, smartphones e outros dispositivos eletrônicos.
Principais Características dos Circuitos Lógicos: Operações Lógicas: Os circuitos lógicos realizam operações baseadas em álgebra booleana, como AND, OR, NOT, XOR, NAND e NOR, que definem como as entradas se relacionam para gerar uma saída.
-
Entradas e Saídas: Um circuito lógico possui entradas que representam dados ou sinais (0s e 1s) e uma ou mais saídas que fornecem o resultado da operação lógica realizada.
-
Composição: Os circuitos lógicos podem ser formados por uma combinação de portas lógicas e outros componentes, como transistores, resistores e capacitores. A configuração dessas portas determina o comportamento do circuito.
-
Simplicidade e Complexidade: Os circuitos lógicos podem ser simples, com apenas algumas portas lógicas, ou muito complexos, envolvendo múltiplas portas e combinações. Circuitos mais complexos são frequentemente usados em funções mais avançadas, como aritmética e controle de processos.
-
Aplicações: Circuitos lógicos são usados em praticamente todos os dispositivos eletrônicos, incluindo computadores, calculadoras, sistemas de controle industrial, dispositivos de comunicação e muito mais. Eles são fundamentais para a construção de sistemas que executam tarefas de computação e controle.
Em resumo, circuitos lógicos são essenciais para a eletrônica digital, permitindo a realização de operações complexas através da combinação de componentes simples que operam com dados binários.
Adder
Um circuito Adder (somador) é um tipo de circuito lógico que realiza a operação de adição de números binários. Os somadores são fundamentais em sistemas digitais e são utilizados em processadores, calculadoras e outros dispositivos eletrônicos que realizam operações aritméticas. Existem diferentes tipos de somadores, sendo os mais comuns:
-
Meio Somador (Half Adder)
Descrição: Um somador de meio é um circuito que soma dois bits de entrada, gerando uma saída de soma e uma saída de carry (transportar).
Entradas: Dois bits (A e B).
Saídas: Soma (S) e Carry (C).
Tabela Verdade:
| A | B | S (Soma)| C (Carry)| |---|-------|---------|----------| | 0 | 0 | 0 | 0 | | 0 | 1 | 1 | 0 | | 1 | 0 | 1 | 0 | | 1 | 1 | 0 | 1 |
-
Somador Completo (Full Adder)
Descrição: Um somador completo é um circuito que soma dois bits de entrada e um bit de carry que pode vir de uma adição anterior. Ele também gera uma saída de soma e uma saída de carry.
Entradas: Três bits (A, B e Carry-in).
Saídas: Soma (S) e Carry-out (C).
Tabela Verdade:
| A | B | Carry-in | S (Soma) | Carry-out (C) | |---|---|-----------|----------|---------------| | 0 | 0 | 0 | 0 | 0 | | 0 | 0 | 1 | 1 | 0 | | 0 | 1 | 0 | 1 | 0 | | 0 | 1 | 1 | 0 | 1 | | 1 | 0 | 0 | 1 | 0 | | 1 | 0 | 1 | 0 | 1 | | 1 | 1 | 0 | 0 | 1 | | 1 | 1 | 1 | 1 | 1 |
-
Circuitos Somadores em Cadeia
Os somadores completos podem ser encadeados para formar circuitos que realizam a adição de números binários com mais de um bit. Por exemplo, para somar dois números de 4 bits, você precisaria de quatro somadores completos, onde a saída de carry de cada somador seria conectada como entrada de carry do próximo.
Importância
Os circuitos adder são essenciais para a aritmética digital e a lógica computacional, permitindo que processadores e outros circuitos realizem operações matemáticas. Eles são a base para a implementação de operações aritméticas em microprocessadores e circuitos integrados.
Exercício: Circuitos Lógicos e Circuitos Adder
Instruções: Responda às perguntas abaixo com base no conteúdo sobre circuitos lógicos e circuitos adder.
-
Sobre Definição de Circuitos Lógicos:
- O que são circuitos lógicos e qual é sua função principal em sistemas digitais?
-
Sobre Operações Lógicas:
- Quais são algumas das operações lógicas que os circuitos lógicos realizam? Cite pelo menos três.
-
Sobre Entradas e Saídas:
- Como são representadas as entradas e saídas em circuitos lógicos? O que os números 0 e 1 representam?
-
Sobre Somadores:
- A). O que é um somador de meio? Quais são suas entradas e saídas principais? Descreva sua tabela verdade. Somador Completo:
- B) O que é um somador completo? Quais são suas entradas e como ele difere de um somador de meio?
-
Sobre Encadeamento de Somadores:
- A) Explique como os somadores completos podem ser usados para somar números binários com mais de um bit. Quantos somadores completos seriam necessários para somar dois números de 4 bits? Importância dos Circuitos Adder:
- B) Por que os circuitos adder são essenciais em sistemas digitais? Dê um exemplo de onde eles são utilizados.
Contribuidores

- João Barros (UmBarril)
- Raphael Sammy (Raphael-Sammy)